SETS
SETS
Set theory was developed by George cantor.
What is Set?
A set is a well-defined collection of elements or objects .
- Well defined means that:
- All the objects in the set should have a common feature or property;
- It should be possible to decide whether any given object belongs to the set or not.
Example:
The collection of all students in your class who are taller than 5 feet.
An object belonging to a set is known as an element of the set.
We usually denote a set by capital letters and the elements of a set by small letters .
Examples:
- Set of odd numbers O = {1, 3, 5, 7, . . . }
- Set of vowels V = { a, e, i, o, u }
Representation of a set:
1) Descriptive form:
a set is represented by a well-defined statement which is enclosed in braces { }.
Example:A set of natural numbers less than 20 is represented by
P = { Natural numbers less than 20}
2) Roaster or Tabular form:
All the elements of a set are listed within curly brackets by putting commas in between two elements is called Roaster form.
In this form elements should not be repeated.
Example:
The set of all letters in the word ASSASSINATION can be written as
Q = {A, I, N, O, S, T}
3) Rule or Set Builder Form:
In set-builder form, the elements are not listed but descriptions of their characteristics within curly brackets.
Examples:
1.R = { 2, 3, 5}.
It can be represented in the set builders form as
R = {x: x is a prime number less than 6}
2.C = {2, 3, 5, 7, 11}, a set of prime numbers less than 13. This set can be denoted as:
C = {x / x is a prime number less than 13}or
C = {x: x is a prime number less than 13}.
Example. Write the following in roster and set builder forms.
(i) The set of all-natural numbers which divide 42.
(ii) The set of natural numbers which are less than 10.
Solution :
(i) Let B be the set of all natural numbers which divide 42. Then, we can write:
B = {1, 2, 3, 6, 7, 14, 21, 42} (Roster form)
B = {x : x is a natural number which divides 42} (Set builder form)
(ii) Let A be the set of all natural numbers which are less than 10. Then, we can write:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9} (Roster form)
B = {x : x is a natural number which is less than 10} (Set builder form)
Example. Write the set B = {x : x is a natural number and x2 < 40} in the roster form.
Solution :
Natural numbers and their squares are starting from 1. When we reach 7, the square is 49 which is greater than 40.
The required numbers are 1, 2, 3, 4, 5, 6.
So, the given set in the roster form is B = {1, 2, 3, 4, 5, 6}.
Exercise 1❯TYPES OF SET:
Null Set:
A set that does not contain any element is called the empty set, or null set, or void set.
The empty set is denoted by the symbol 𝜙 or { }.
Examples:
(i) A = {x : x is natural number smaller than 1}
(ii) D = {x : x is a odd prime number divisible by 2}
(iii) B = {x : 1 < x < 2, x is a natural number}
(iv) E = {x : x2 – 2 = 0 and x is a rational number}
(v) C = {x : x2 = 4, x is odd}
Note :
𝜙 and {0} are two different sets. {0} is a set containing the single element 0 while {} is null set
Universal Set:
A universal set is the collection of all objects in a particular context.
It is denoted by 'μ'. It is usually represented by rectangles.
Examples:
(i)For a selection of any school team, the students of your school are considered as the universal set.
(ii)If we want to study the various groups of people in our country, the universal set is the set of all people in India.
Subset:
If every element of a set A is also an element of set B, then the set A is said to be a subset of set B. It is represented as A⊂B.
Example:
If A = {2, 6, 10}; B = {2, 4, 6, 8, 10, 12, 14}, then A is a subset of B (i.e. A⊂B)
we can write the definition of the subset as follows:
A ⊂ B if a ∈A ⇒ a ∈ B, where A, B are two sets.
We read the above statement as “A is a subset of B if 'a' is an element of A implies that 'a' is also an element of B”.
‘⇒’ means implies.
Note:
- Every Set is a subset of itself ( A⊂ A, B ⊂ B)
- Empty Set is a subset of every set
- If A⊂B and B⊂C then A ⊂ C (Transitive property)
- A⊂B and B⊂A ⟺ A = B (Anti symmetric property)
- If the number of elements in a set is 𝑛, then the number of possible subsets for the set is 2𝑛.
Venn Diagrams:
Venn-Euler diagram or Simply Venn diagram is a way of representing the relationships between sets. These diagrams consist of rectangles and closed curves usually circles.
BASIC OPERATIONS ON SETS
Union of sets:
The union of A and B is the Set that contains all the elements of A and the elements of B and the common elements being taken only once.
The symbol 'U' is used to denote the union. Symbolically, we write AUB and read as 'A' union 'B'.
The union of the sets can be represented by a Venn-diagram as shown (shaded portion)

Example:
A = {1, 2, 3, 4, 5}; B = {2, 4, 6, 8, 10}
Then A U B = {1, 2, 3, 4, 5} U {2, 4, 6, 8, 10}
= {1, 2, 3, 4, 5, 6, 8, 10}
The set builder form of A U B is
A ∪ B = {x : x ∈ A or x ∈ B}
Example.
Suppose A is the set of students in your class who were absent on Tuesday and B the set of students who were absent on Wednesday. Then, A = {Roja, Ramu, Ravi} and B = {Ramu, Preethi, Haneef} find the set of students who were absent on either Tuesday or Wednesday.
Solution:
A ∪ B ={Roja, Ramu, Ravi}∪ {Ramu, Preethi, Haneef}
={Roja, Ramu, Raheem, Prudhvi, Preethi}
Example-1. Let A = {2, 5, 6, 8} and B = {5, 7, 9, 1}. Find A ∪ B.
Solution :
A ∪ B = {1, 2, 5, 6, 7, 8, 9}.
Note that the common element 5 was taken only once while writing A ∪ B.
Example-2. Let A = {a, e, i, o, u} and B = {a, i, u}. Show that A ∪ B = A.
Solution :
We have A ∪ B = {a, e, i, o, u} = A.
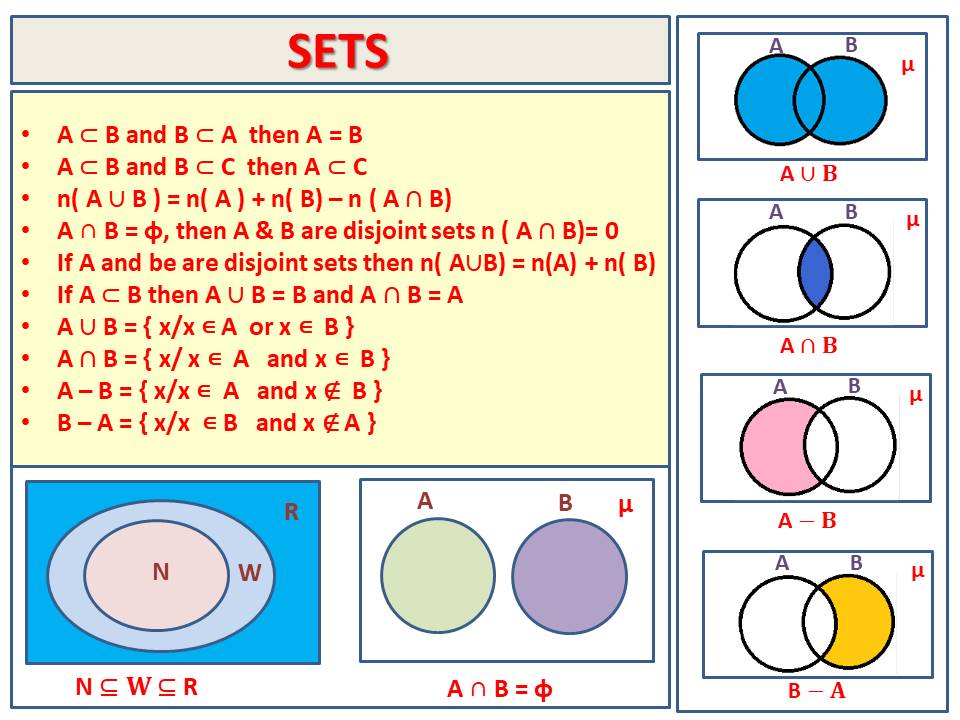
Example-3.
Illustrate A ∪ B in Venn diagrams where. A = {1, 2, 3, 4} and B = {2, 4, 6, 8} A ∪ B = {1, 2, 3, 4, 6, 8}
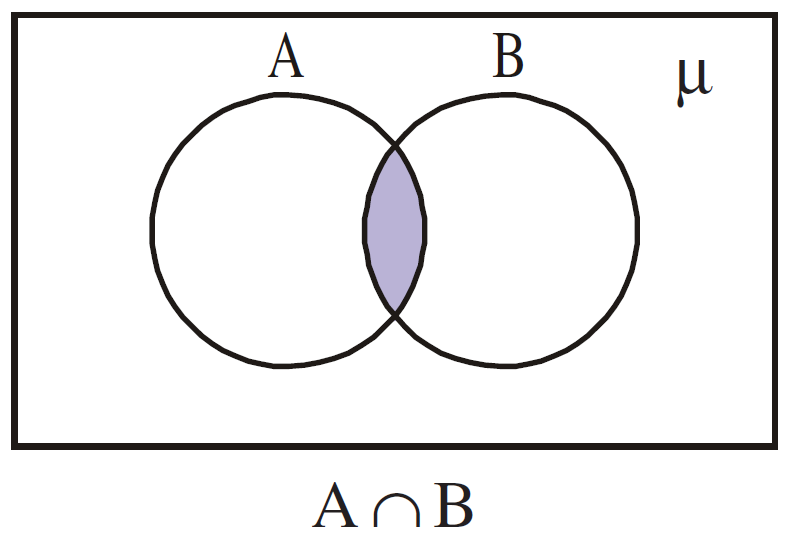
Intersection of sets:
The intersection of A and B is the Set in which the elements that are common to both A and B.
The Symbol '⋂' is used to denote the 'intersection'. Symbolically we write "A⋂B" and read as "A intersection B".
Example:
A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8, 10}
Then A ⋂ B = {1, 2, 3, 4, 5} ⋂ {2, 4, 6, 8,10}= {2,4}
The set builder form of A ⋂ B is
A⋂B = {𝒙: 𝒙𝝐𝑨 and 𝒙𝝐𝑩}
Example-4. Find A ∩ B when A = {5, 6, 7, 8} and B = {7, 8, 9, 10}.
Solution :
The common elements in both A and B are 7, 8.
∴ A ∩ B = {7, 8}.
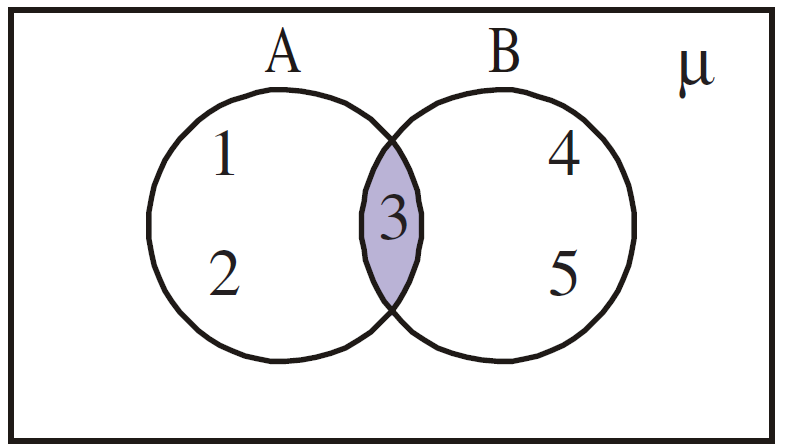
Example-5. Illustrate A ∩ B in Venn-diagrams where A = {1, 2, 3} and B = {3, 4, 5}
Solution :
The intersection of A and B can be illustrated in the Venn diagram as follows:

Disjoint Sets:
The sets A and B are said to be disjoint if they have no elements in common.
Example:
A = {1, 3, 5, 7, . . . .} ; B = {2, 4, 6 , 8, . . . .}
Here A and B have no common elements so these sets are called disjoint sets.
If A, B are disjoint sets then A⋂B = 𝜙
If A⋂B = 𝜙, then n(A⋂B) = 0.
A {1, 3, 5, 7} and B = {2, 4, 6, 8}. We see that there are no common elements in A and B. Such sets are known as disjoint sets. The disjoint sets can be represented by means of the Venn diagram as follows:

Difference of sets:
The difference between Sets A and B is the set of elements which belong to A but do not belong to B.
We denote the difference of A and B by A-B or simply "A minus B".
Similarly, B-A is the set whose elements belong to B but not belong to A.
Example:
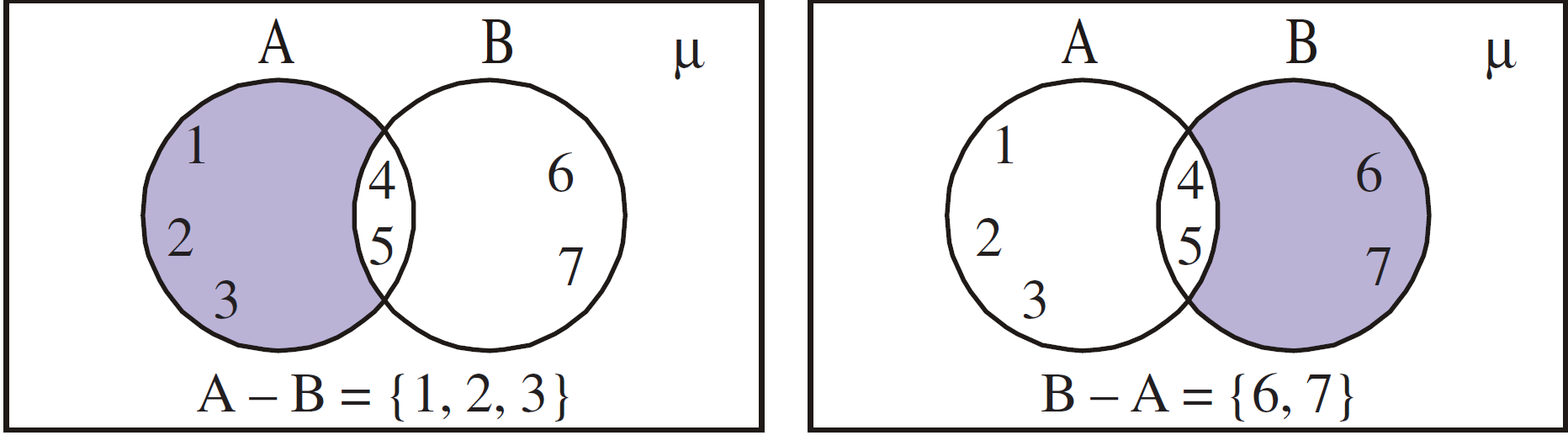
If A= {1, 2, 3, 4, 5} and B = {4, 5, 6, 7} then
A - B = {1, 2, 3, 4, 5} - {4, 5, 6, 7} = {1, 2, 3},
B - A = {4, 5, 6, 7} - {1, 2, 3, 4, 5} = { 6, 7}
The set builder forms of A − B and B − A are
A-B = {x: x 𝝐 A and x ∉ B}
B-A = {x: x 𝝐 B and x∉ B}
Example-6. Let A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7}. Find A – B.
Solution :
Given A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7}.
Only the elements which are in A but not in B should be taken.
∴ A – B = {1, 2, 3} (Since 4, 5 are the elements in B they are not taken.)
Similarly for B – A, the elements which are only in B are taken.
∴ B – A = {6, 7} (4, 5 are the elements in A).
Note that A – B ≠ B – A
The Venn diagram of A-B is as shown.
Exercise 2❯
Equal Sets:
Two sets A and B are said to be 'equal' if they have exactly the same elements.
If Two sets A and B are said to be equal if every element in A belongs to B and every element in B belongs to A.
If A and B are equal sets, than we write A = B.
Example-7. Consider the following sets: A = {p, q, r} B = {q, p, r}. Are they equal?
Solution:
In the above sets, every element of A is also an element of B. ∴ A ⊂ B.
Similarly every element of B is also in A. ∴ B ⊂ A.
Thus, we can also write that if B ⊂ A and A ⊂ B ⇔A = B.
Here ⇔ is the symbol for two way implication and is usually read as, if and only if (briefly written as “iff”).
Examples-8. If A = {1, 2, 3, ….} and N is a set of natural numbers, check whether A and N are equal?
Solution :
A and N are the set of Natural numbers. The elements are same in both the sets.
Therefore the sets A and N are equal sets or A = N.
Example-9. Consider the sets A = {p, q, r, s} and B = {1, 2, 3, 4}. Are they equal?
Solution :
A and B do not contain the same elements.
So, A ≠ B.
Example-10. Let A be the set of prime numbers less than 6 and P the set of prime factors of 30. Check if A and P are equal.
Solution :
The set of prime numbers less than 6, A = { 2,3,5}
The prime factors of 30 are 2, 3 and 5. So, P = { 2,3,5}
Since the elements of A are the same as the elements of P, therefore, A and P are equal.
Example-11. Show that the sets A and B are equal,
where A = {x : x is a letter in the word ‘ASSASSINATION’} B = {x : x is a letter in the word STATION}
Solution :
Given, A = {x : x is a letter in the word ‘ASSASSINATION’}
This set A can also be written as A = {A,S,I,N,T,O}
B = {x : x is a letter in the word STATION}
‘B’ can also be written as B = {A,S,I,N,T,O}
So, the elements of A nd B are same and A = B
Example 12
Consider the sets 𝜙 , A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}. Insert the symbol ⊂ or ⊄ between each of the following pair of sets. (i)𝜙 ….. B (ii) A ….. B (iii) A ….. C (iv) B ….. C
Solution :
(i) 𝜙 ⊂ B, as 𝜙 is a subset of every set.
(ii) A ⊄ B, for 3 ∈ A but 3 ∉ B.
(iii) A ⊂ C as 1, 3 ∈A also belong to C.
(iv) B ⊂ C as each element of B is also an element of C.
Exercise 3❯
Finite Set:
A set contain finite number(countable) of elements then it is called finite set.
Examples:
(i) A = {the students of your school}
(ii) L = {p,q,r,s}
(iii) B = { 5, 10, 15, 20, 25, 30}
Null set is a finite set because it has zero elements.
Infinite Set:
A set cotain infinite number(uncountable) of elements then it is called an infinite set.
Examples:
(i) C = {5, 10, 15, 20, 25, 30 . . . . . . .}
(ii) B = {x : x is an even number}
iii) J = {x : x is a multiple of 7}
Consider some more examples :
(i) Let ‘W’ be the set of the days of the week. Then W is finite.
(ii) Let ‘S’ be the set of solutions of the equation x2 – 16 = 0. Then S is finite.
(iii) Let ‘G’ be the set of points on a line. Then G is infinite.
Example-13. State which of the following sets are finite or infinite.
(i) {x : x ∈ N and (x − 1) (x − 2) = 0}
(ii) {x : x ∈ N and x2 = 4}
(iii) {x : x ∈ N and 2x − 2 = 0}
(iv) {x : x ∈ N and x is prime}
(v) {x : x ∈ N and x is odd}
Solution :
(i) x can take the values 1 or 2 in the given case. The set is {1,2}. Hence, it is finite.
(ii) x2 = 4, implies that x = +2 or −2. But x ∈ N or x is a natural number so the set is{2}. Hence, it is finite.
(iii) In a given set x = 1 and 1 ∈ N. Hence, it is finite.
(iv) The given set is the set of all prime numbers. There are infinitely many prime numbers. Hence, set is infinite.
(v) Since there are infinite number of odd numbers, hence the set is infinite.
Cardinal Number:
Number of elements in a Set is called the cardinal number of the set. n(A) represents cardinal number of set 'A'.
Example:
A = {1, 2, 4}; B = {6, 7, 8, 9, 10}; C = {x : x is a alphabet in the word "INDIA"}
Here,
Number of elements in set A = 3.
Number of elements in set B = 5.
Number of elements in set C = 4 (In the set C, the element ‘I’ repeats twice.).
The cardinal number of the set A is denoted as n(A) = 3.
Similarly, n(B) = 5 and n(C) = 4.
Note:
There are no elements in a null set.
The cardinal number of that set is 0. ∴ n(𝜙 )= 0
Example-14. If A = {1, 2, 3,4,5}; B = {2,4,6,8} then find n(A ∪ B).
Solution :
The set A contains three distinct elements ∴ n(A) = 5
and the set B contains three distinct elements ∴ n(B) = 4
A ∪ B = {1,2, 3, 4, 5, 6, 8}
∴n(A ∪ B) = 7
Example. If A = {1, 2, 3}; B = {a, b, c} then find n(A) and n(B).
Solution :
The set A contains three distinct elements ∴ n(A) = 3
and the set B contains three distinct elements ∴ n(B) = 3
Example.
Observe the following
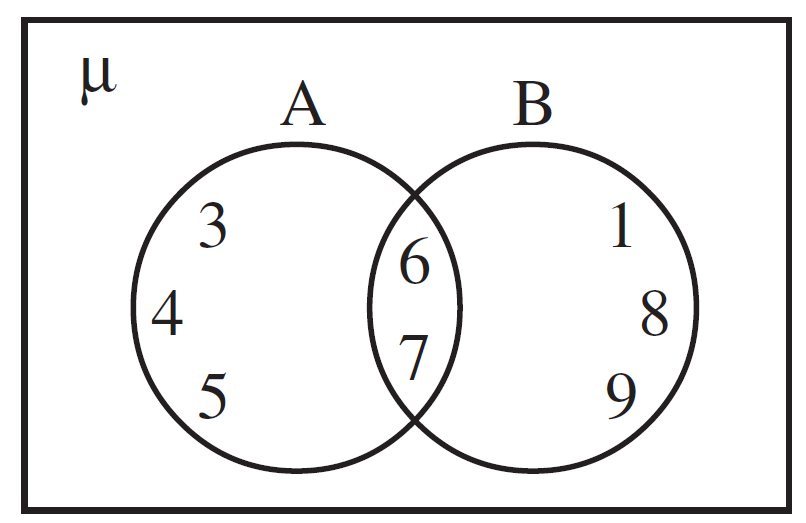
A = {3, 4, 5, 6, 7} ∴ n(A) = 5
B = {1, 6, 7, 8, 9} ∴ n(B) = 5
A ∪ B = {1, 3, 4, 5, 6, 7, 8, 9}
∴n(A ∪ B) = 8
A ∩ B = {6, 7} ∴ n(A ∩ B) = 2
∴ n(A ∪ B) = 5 + 5 – 2 = 8
We observe that
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)Exercise 4❯
సమితులు
సమితి వాదాన్ని అబివృద్ది చేసింది జార్జ్ కాంటర్.
సమితి అంటే ఏమిటి ?
సునిర్వచిత వస్తువుల సముదాయాన్ని సమితి అంటారు .
- సునిర్వచితం అంటే :
- సమితిలోని మూలకాలాన్ని ఒక సామాన్య ధర్మాన్ని లేక పోలికను కలిగి వుండాలి
- ఏదైనా ఒక వస్తువు సమితికి చెందినది లేనిది నిర్ధారించగలగాలి.
ఉదాహరణ :
మీ తరగతి లో 5 అడుగుల కంటే ఎక్కువ ఎత్తు ఉన్న విధ్యార్డుల సమితి.
సమితి కి చెందిన వస్తువులను మూలకాలు అంటారు.
సాధారణంగా సమితిని ఆంగ్లం లోని పెద్ద అక్షరాల చేతను మూలకాలను చిన్న అక్షరాల చేతను సూచిస్తాము.
ఉదాహరణ :
- బేసి సంఖ్యల సమితి O = {1, 3, 5, 7, . . . }
- ఆంగ్ల అక్షరలలోని అచ్చుల సమితి V = { a, e, i, o, u }
సమితిని సూచించే విధానం :
1) వివరణాత్మక రూపం:
సమితిని ఖచ్చితంగా నిర్వచించబడిన ఒక వాక్యంలో { } లో రాస్తాము.
ఉదాహరణ :20 కంటే తక్కువైన సహజ సంఖ్యల సమితి
ుP = { 20 కంటే తక్కువైన సహజ సంఖ్యలు }
2) రోస్టర్ లేదా జాబితా రూపం:
సమితిలోని అన్నీ మూలకాలను { } బ్రాకెట్ల లో కామాలతో వేరు చేస్తూ రాసే రూపాన్ని జాబితా రూపం అంటారు.
ఇందులో ఒకే మూలకాన్ని మరలా,మరలా రాయకూడదు
ఉదాహరణ :
Q అనేది ASSASSINATION అనే పదం లోని అక్షరాల సమితి
Q = {A, I, N, O, S, T}
3) సమితి నిర్మాణ రూపం :
మూలకాలకు చెందిన సామాన్య ధర్మాన్ని లేక లక్షణాన్ని { } లో రాసే పద్దతిని సమితి నిర్మాణ రూపం అంటారు
ఉదాహరణలు
1.R = { 2, 3, 5}.
దీనిని సమితి నిర్మాణ రూపం లో రాస్తే
R = {: x: x అనేది 6 కంటే తక్కువైన ప్రధాన సంఖ్య }
2.C = {2, 3, 5, 7, 11}, అనేది 13 కంటే తక్కువైన ప్రధాన సంఖ్యలు కలిగిన సమితి దీనిని ఈ క్రింది విధంగా సూచిస్తాము
C = {x / x అనేది 13 కంటే తక్కువైన ప్రధాన సంఖ్య } లేదా
C = {x: x అనేది 13 కంటే తక్కువైన ప్రధాన సంఖ్య }.
ఉదాహరణ : ఈ క్రింది వాటిని సమితి నిర్మాణ రూపం లో మరియు జాబితా రూపం లో రాయండి
(i) 42 ను భాగించే సంఖ్యల సమితి.
(ii) 10 కంటే తక్కువైన సహజ సంఖ్యల సమితి.
సాధన :
(i)B అనేది 42 ను భాగించే సంఖ్యల సమితి అనుకుందాం. అయితే :
B = {1, 2, 3, 6, 7, 14, 21, 42} (జాబితా రూపం )
B = {x : x అనేది 42 ను భాగించే సహజ సంఖ్య } ( సమితి నిర్మాణ రూపం )
(ii) A అనేది 10 కంటే తక్కువైన సహజ సంఖ్యల సమితి అయితే
A = {1, 2, 3, 4, 5, 6, 7, 8, 9} (జాబితా రూపం )
B = {x : x అనేది 10 కంటే తక్కువైన సహజ సంఖ్య } ( సమితి నిర్మాణ రూపం )
ఉదాహరణ: B = {x : x అనేది సహజ సంఖ్య మరియు x2 < 40} దీనిని జాబితా రూపంలో రౌయండి.
సాధన:
40 కంటే తక్కువైన సహజ సంఖ్యల వర్గాలు వరుసగా 1,4,9,16,25,36 వీటి యొక్క వర్గమూలాలు 1, 2, 3, 4, 5, 6.
వీటిని జాబితా రూపంలో రాస్తే B = {1, 2, 3, 4, 5, 6}.
Exercise 1❯సమితులు-రకాలు:
శూన్య సమితి :
ఒక సమితి మూలకాలు ఏవి లేకపోతే ఆ సమితిని శూన్య సమితి అందురు .
శూన్య సమితి ని 𝜙 లేదా { } గుర్తులతో సూచిస్తారు
ఉదాహరణ s:
(i) A = {x : x అనేది 1 కంటే తక్కువైన సహజ సంఖ్య }
(ii) D = {x : x అనేది 2 చే భాగించగ శేషం 0 వచ్చే బేసి సంఖ్య }
(iii) B = {x : 1 < x < 2, x ఒక సహజ సంఖ్య }
(iv) E = {x : x2 – 2 = 0 మరియు x ఒక అకరణీయ సంఖ్య }
(v) C = {x : x2 = 4, x ఒక బేసి సంఖ్య }
గమనిక :
𝜙 మరియు {0} లు రెండు వేర్వేరు సమితులు . సమితి {0} లో ఒకే ఒక మూలకం 0 ఉంది. {} శూన్య సమితి
విశ్వ సమితి:
సార్వత్రిక సమితి అనేది ఒక నిర్దిష్ట పరిధిలో అన్ని వస్తువుల సమాహారం.
దీనిని 'μ'తో సూచిస్తారు.దీనిని సహజంగా దీర్ఘ చతురస్రం తో సూచిస్తారు.
ఉదాహరణ:
(i).ఒక పాఠశాల లోని విద్యార్డులతో ఒక టీం చేయాలంటే మొత్తం విద్యార్డులు విశ్వ సమితి లోకి వస్తారు
(ii) మన రాష్ట్రం లోని వివిధ రకాలైన ప్రజా సమూహాలను అధ్యయనం చేసేటప్పుడు రాష్ట్ర ప్రజలందరూ విశ్వ సమితిలోకి వస్తారు.
ఉపసమితి:
A అనే సమితి లోని ప్రతి మూలకం B అనే సమితి లో వుంటే A సమితి ని B సమితి కి ఉపసమితి అంటారు దీనిని A⊂B తో సూచిస్తారు.
ఉదాహరణ:
If A = {2, 6, 10}; B = {2, 4, 6, 8, 10, 12, 14}, A, B కి ఉపసమితి అవుతుంది (i.e. A⊂B)
ఉపసమితి యొక్క నిర్వచనం :
A, B లు రెండు సమితులు మరియు a ∈A ⇒ a ∈ B అయితే A ⊂ B అవుతుంది.
A ⊂ B ను “A is subset of B అని చదువుతాము.
గమనిక :
- ప్రతి సమితి దానికదే ఉపసమితి అవుతుంది ( A⊂ A, B ⊂ B)
- .శూన్య సమితి ప్రతి సమితికి ఉపసమితి అవుతుంది.
- A⊂B మరియు B⊂C అయితే A ⊂ C అవుతుంది, (సంక్రమణ ధర్మం)
- A⊂B మరియు B⊂A ⟺ A = B
- ఒక సమితి లోని మూలకల సంఖ్య 𝑛, అయితే దానికి గల ఉపసమితుల సంఖ్య 2𝑛.
వెన్ చిత్రాలు:
సమితుల మధ్య సంబంధాలను సూచించటానికి వెన్ -ఆయిలర్ చిత్రాలను ఉపయోగిస్తాం ఈ చిత్రాలలో దీర్ఘ చతురస్రాలు మరియు వృత్తాలు వుంటాయి

సమితులలో ప్రాధమిక పరిక్రియలు
సమితుల సమ్మేళనం :
A మరియు B రెండు సమితులలోని మూలకాలను ఒకసారి మాత్రమే తీసుకుంటే దానిని A మరియు B సమితుల సమ్మేళనం అంటారు.
సమితుల సమ్మేళనానికి 'U' అనే గుర్తును వాడుతారు. AUB అని రాస్తారు మరియు 'A' union 'B' గా చదువుతారు .
A,B సమితుల సమ్మేళనాన్ని వెన్ చిత్రం లో ఈ విధంగా చూపుతాము (షేడ్ చేసిన భాగం )

ఉదాహరణ :
A = {1, 2, 3, 4, 5}; B = {2, 4, 6, 8, 10}
A U B = {1, 2, 3, 4, 5} U {2, 4, 6, 8, 10}
= {1, 2, 3, 4, 5, 6, 8, 10}
A U B యొక్క సమితి నిర్మాణ రూపం
A ∪ B = {x : x ∈ A or x ∈ B}
ఉదాహరణ .
A మంగళవారం హాజరు కాని వారి సమితి మరియు B బుధవారం హాజరు కాని వారి సమితి అయితే , A = {రోజా , రాము , రవి } B = {రాము , ప్రీతి , హనీఫ్} మంగళవారం కాని లేదా బుధవారం కాని హాజరు కానివారిని కనుగొనండి .
సాధన :
A ∪ B ={రోజా , రాము , రవి }∪ {రాము , ప్రీతి , హనీఫ్ }
={రోజా , రాము , రవి , ప్రీతి , హనీఫ్}
ఉదాహరణ-1. A = {2, 5, 6, 8} మరియు B = {5, 7, 9, 1}అయితే A ∪ B ని కనుగొనండి .
సాధన :
A ∪ B = {1, 2, 5, 6, 7, 8, 9}.
ఉదాహరణ-2. A = {a, e, i, o, u} మరియు B = {a, i, u} అయితే A ∪ B = A అని చూపండి.
సాధన :
A ∪ B = {a, e, i, o, u} ∪ {a, i, u}={a, e, i, o, u}= A.
ఉదాహరణ -3.
A ∪ B ని వెన్ చిత్రం ద్వారా చూపండి. A = {1, 2, 3, 4} మరియ B = {2, 4, 6, 8} A ∪ B = {1, 2, 3, 4, 6, 8}

సమితుల ఛేదనం:
A సమితి మరియు B సమితి లలో ఉన్న ఉమ్మడి మూలకాలను A,B సమితుల ఛేదనం అంటారు.
సమితుల చేదనాన్ని సూచించటానికి '⋂' గుర్తును వాడతారు'. దీనిని "A⋂B" అని రాస్తాము "A intersection B" అని చదువుతాము .

ఉదాహరణ:
A = {1, 2, 3, 4, 5} మరియ B = {2, 4, 6, 8, 10}
A ⋂ B = {1, 2, 3, 4, 5} ⋂ {2, 4, 6, 8,10}= {2,4}
A ⋂ B యొక్క సమితి నిర్మాణ రూపం
A⋂B = {𝒙: 𝒙𝝐𝑨 మరియ 𝒙𝝐𝑩}
ఉదాహరణ-4. A = {5, 6, 7, 8} మరియ B = {7, 8, 9, 10} అయితే A ∩ B ని కనుగొనుము.
సాధన :
A మరియు B లోని ఉమ్మడి మూలకాలు 7, 8.
∴ A ∩ B = {7, 8}.
ఉదాహరణ -5 : A = {1, 2, 3} మరియ B = {3, 4, 5} అయితే A ∩ B ని వెన్ చిత్రం ద్వారా చూపండి.
సాధన :
A మరియు B ల ఛేదన సమితి

వియుక్త సమితులు :
A మరియు B లలో ఉమ్మడి మూలకాలు ఏమి లేకపోతే A , B లను వియుక్త సమితులు అంటారు .
ఉదాహరణ :
A = {1, 3, 5, 7, . . . .} ; B = {2, 4, 6 , 8, . . . .}
A మరియు B లలో ఉమ్మడి మూలకాలు ఏమి లేవు కావున ఇవి వియుక్త సమితులు అందురు.
A, B లు వియుక్త సమితులు అయితే A⋂B = 𝜙
A⋂B = 𝜙, అయితే n(A⋂B) = 0.
A = {1, 3, 5, 7} మరియు B = {2, 4, 6, 8}. A మరియు B లలో ఉమ్మడి మూలకాలు ఏమి లేవు కావున ఇవి వియుక్త సమితులు.వీటిని వెన్ చిత్రాలలో ఇలా చూపుతాము

సమితుల భేదం :
A మరియు B ల భేదం అంటే మూలకాలు A కు చెందుతాయి మరియు B కు చెందవు.
దీనిని A-B అని రాస్తాము "A minus B" అని చదువుతాము.
అదేవిధంగా , B-A B లో వుండి A లో లేని మూలకాల సమితి.
ఉదాహరణ :
A= {1, 2, 3, 4, 5} మరియు B = {4, 5, 6, 7} అయితే
A - B = {1, 2, 3, 4, 5} - {4, 5, 6, 7} = {1, 2, 3},
B - A = {4, 5, 6, 7} - {1, 2, 3, 4, 5} = { 6, 7}
A − B మరియు B − A ల యొక్క సమితి నిర్మాణ రూపం
A-B = {x: x 𝝐 A మరియు x ∉ B}
B-A = {x: x 𝝐 B మరియు x∉ B}
ఉదాహరణ-6. Let A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7}. A – B కనుగొనండి.
సాధన :
A = {1, 2, 3, 4, 5} మరియు B = {4, 5, 6, 7}.
Aలో మాత్రమే వుంది B లో లేని మూలకాలను తీసుకోవాలి .
∴ A – B = {1, 2, 3} ( 4, 5 లు B లో వున్నాయి.)
అదేవిధంగా B – A, Bలో మాత్రమే వున్న మూలకాలను తీసుకోవాలి.
∴ B – A = {6, 7} (4, 5 లు A లో వున్నాయి ).
A – B ≠ B – A
A-B ల వెన్ చిత్రం .

Exercise 2❯
సమ సమితులు :
రెండు సమితులు A మరియు B లు సమానం కావాలంటే రెండింటిలో ఖచ్చితంగా ఒకే మూలకాలు వుండాలి.
రెండు సమితులు సమానమైతే A సమితి లోని మూలకాలు మొత్తం B సమితి లో B సమితి లోని మూలకాలు మొత్తం A సమితి లో వుండాలి
A మరియు B లు సమ సమితులయితే A = B అని రాస్తాము .
ఉదాహరణ-7. A = {p, q, r} B = {q, p, r}. ఇవి రెండు సమసమితులేన?
సాధన :
Aలో వున్న ప్రతి మూలకం B లో ఉంది. ∴ A ⊂ B.
అదేవిధంగా B లో వున్న ప్రతి మూలకం A లో వుంది. ∴ B ⊂ A.
కావున B ⊂ A మరియు A ⊂ B ⇔A = B.
ఇక్కడ ⇔ గుర్తు రెండు వైపులా వర్తిస్తుంది.దీనిని if మరియ only if ( “iff”) అని చదువుతాము.
ఉదాహరణ-8. If A = {1, 2, 3, ….} మరియ N సహజ సంఖ్య సమితి , A మరియు N లు సమనమేన ?
సాధన :
Aమరియు N లు రెండు సహజ సంఖ్య సమితులను సూచిస్తాయి వీటిలోని మూలకాలు సమానం .
కావున A మరియు N లు సమ సమితులు లేదా A = N.
ఉదాహరణ-9. A = {p, q, r, s} మరియు B = {1, 2, 3, 4}లు రెండు సమితులు . ఇవి రెండు సమానమా ?
సాధన :
Aమరియు B ఒకే మూలకాలను కలిగి లేవు .
కావున , A ≠ B.
ఉదాహరణ-10. A అనేది 6 కంటే తక్కువైన ప్రధాన సంఖ్య సమితి మరియు P అనేది 30 యొక్క ప్రధాన్ కారణాంకాల సమితి . A మరియు P లు సమనమేన.
సాధన :
6 కంటే తక్కువైన ప్రధాన సంఖ్య , A = { 2,3,5}
30 యొక్క ప్రధాన కారణాంకాలు 2, 3 మరియు 5. కావున P = { 2,3,5}
A,P లలో మూలకాలు ఒకటే కావున A మరియు P లు సమానం .
ఉదాహరణ-11. A మరియు B లు సమానమని చూపండి.
A = {x : x అనేది ‘ASSASSINATION’అనే పదం లోని అక్షరం } B = {x : x అనేది STATION అనే పదం లోని అక్షరం }
సాధన :
A = {x : x అనేది ‘ASSASSINATION’అనే పదం లోని అక్షరం}
A = {A,S,I,N,T,O}
B = {x : x అనేది STATION అనే పదం లోని అక్షరం }
B = {A,S,I,N,T,O}
A మరియు B లోని మూలకాలు ఒకటే కావున A = B
ఉదాహరణ- 12
𝜙 , A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9} సమీతులను గమనించండి . ⊂ లేదా ⊄ క్రింద ఇచ్చిన సమితుల మధ్య ఈ గుర్తులను వుంచండి (i)𝜙 ….. B (ii) A ….. B (iii) A ….. C (iv) B ….. C
సాధన :
(i) 𝜙 ⊂ B, 𝜙 అనేది ప్రతి సమితికి ఉపసమితి .
(ii) 3 ∈ A కానీ 3 ∉ B కావున A ⊄ B.
(iii) 1, 3 ∈A మరియు C కావున A ⊂ C.
(iv) B లో వున్న ప్రతి మూలకం C లో ఉంది కావున B ⊂ C .
Exercise 3❯
పరిమిత సమితి:
ఒక సమితి లోని మూలకాలను లెక్కించగలిగితే దానిని పరిమిత సమితి అంటారు .
ఉదాహరణ s:
(i) A = {మీ పాఠశాల లోని విధ్యార్ధులు }
(ii) L = {p,q,r,s}
(iii) B = { 5, 10, 15, 20, 25, 30}
శూన్య సమితి పరిమిత సమితి కారణం అందులో మూలకాల సంఖ్య 0.
అపరిమిత సమితి:
ఒక సమితిలోని మూలకాలను లెక్కించటానికి వీలుకాకపోతే దానిని అపరిమిత సమితి అంటారు .
ఉదాహరణ :
(i) C = {5, 10, 15, 20, 25, 30 . . . . . . .}
(ii) B = {x : x is an even number}
iii) J = {x : x is a multiple of 7}
మరి కొన్ని ఉదాహరణలు :
(i) ‘W’ అనేది వారం లో రోజుల సమితి . వారం లో రోజులు 7 కావున W అనేది పరిమిత సమితి .
(ii) ‘S’ అనేది x2 – 16 = 0 యొక్క సాధనాల సమితి . దీనికి సాధనాలు 2 మాత్రమే కావున S అనేది పరిమిత సమితి .
(iii) ‘G’ అనేది ఒక రేఖ పైన బిందువుల సమితి . రేఖ పై బిందువులను లెక్కించలేము కావున G అపరిమిత సమితి అవుతుంది .
ఉదాహరణ -13. క్రింది సమితులలో ఏవి పరిమిత సమితులు ఏవి అపరిమిత సమితులు .
(i) {x : x ∈ N మరియ (x − 1) (x − 2) = 0}
(ii) {x : x ∈ N మరియ x2 = 4}
(iii) {x : x ∈ N మరియ 2x − 2 = 0}
(iv) {x : x ∈ N మరియ x ప్రధాన సంఖ్య }
(v) {x : x ∈ N మరియ x బేసిసంఖ్య }
సాధన :
(i) x యొక్క విలువలు 1 లేదా 2. సమితి {1,2}. కావున ఇది పరిమిత సమితి .
(ii) x2 = 4, దీని నుండి x = +2 or −2. కానీ x ∈ N లేదా x ఒక సహజ సంఖ్య కావున సమితి {2}. కావున ఇది పరిమిత సమితి .
(iii) ఇచ్చిన సమితి లో x = 1 మరియ 1 ∈ N. కావున ఇది పరిమిత సమితి .
(iv) ఇచ్చిన సమితి ప్రధాన సంఖ్యల సమితి . వీటి సంఖ్య చెప్పలేము కావున ఇది అపరిమిత సమితి .
(v) ఇందులో అనంతమైన బేసి సంఖ్యలు వున్నాయి కావున ఇది అపరిమిత సమితి .
కార్డినల్ సంఖ్య :
సమితిలోని మూలకాల సంఖ్యను సమితి యొక్క కార్డినల్ సంఖ్య అంటారు. A సమితి యొక్క కార్డినల్ సంఖ్యను n(A) తో సూచిస్తారు.
ఉదాహరణ:
A = {1, 2, 4}; B = {6, 7, 8, 9, 10}; C = {x : x అనేది "INDIA" అనే పదం లోని అక్షరం }
Here,
A లోని మూలకాల సంఖ్య = 3.
B లోని మూలకాల సంఖ = 5.
C లోని మూలకాల సంఖ్య = 4
n(A) = 3
n(B) = 5 మరియ n(C) = 4.
గమనిక :
శూన్య సమితి లో మూలకాలు వుండవు.
కావున దీని యొక్క కార్డినల్ సంఖ్య 0. ∴ n(𝜙 )= 0
ఉదాహరణ-14. If A = {1, 2, 3,4,5}; B = {2,4,6,8} అయితే n(A ∪ B) కనుగొనండి .
సాధన :
A లోని మూలకాల సంఖ్య =5 ∴ n(A) = 5
మరియ B లోని మూలకాల సంఖ్య = 3 ∴ n(B) = 4
A ∪ B = {1,2, 3, 4, 5, 6, 8}
∴n(A ∪ B) = 7
ఉదాహరణ. If A = {1, 2, 3}; B = {a, b, c} అయితే n(A) మరియ n(B) ని కనుగొనుము .
సాధన :
A లోని మూలకాల సంఖ్య = 3 ∴ n(A) = 3
మరియ B లోని మూలకాల సంఖ్య = 3 ∴ n(B) = 3
ఉదాహరణ.
గమనించండి
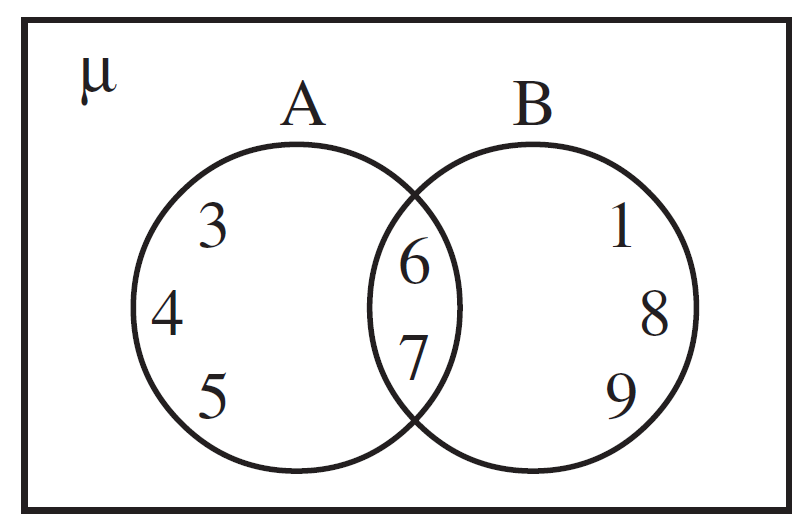
A = {3, 4, 5, 6, 7} ∴ n(A) = 5
B = {1, 6, 7, 8, 9} ∴ n(B) = 5
A ∪ B = {1, 3, 4, 5, 6, 7, 8, 9}
∴n(A ∪ B) = 8
A ∩ B = {6, 7} ∴ n(A ∩ B) = 2
∴ n(A ∪ B) = 5 + 5 – 2 = 8
Exercise 4❯

Post a Comment