2. FRACTIONS AND DECIMALS

The fraction with denominators 10, 100, 1000, 10000, … etc. is decimal fractions or decimal numbers.
The fraction `1/10`can be written as 0.1 in decimal form (read as zero point one).
So, a decimal number is another way of expression of a fraction.

Observe the following table and fill in the blanks.

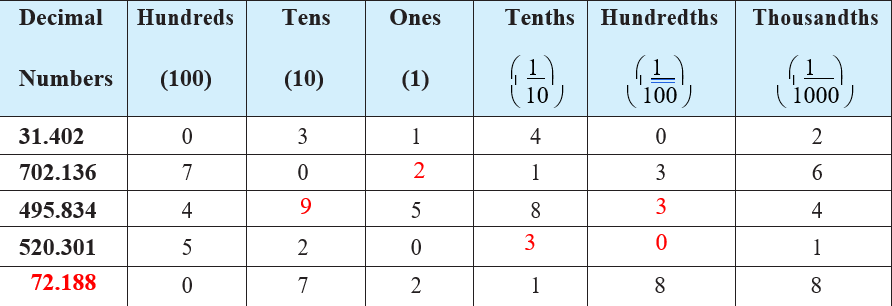
Expanded form of 31.402 is
31.402=30+1+`4/10+0/100+2/1000`

Place value of 4 in 31.402 is `4/10`

Add or subtract decimals:

The decimal numbers are written one under the other with the decimal points lined up. Add or subtract as you would do to whole numbers, then, place the decimal place in the result in line with the other decimal points.

Example:

Multiplication of Decimal number with Whole number :

Method - 1: (Converting decimal in to a fraction)
3 × 1.5 = 3 × `15/10=45/10`=4.5.

Method - 2:(Multiply and put decimals)
3 × 1.5
Step 1 : Multiply whole numbers ignoring decimals.
3 × 15 = 45

Step 2 : Then mark the decimal point to the product from right most to left according to the number of decimal places in the given decimal. Here only one decimal place is there.
∴ 3 × 1.5 = 4.5

Multiplication of two decimal numbers:

Method - 1: (Converting decimal in to a fraction)
0.4× 0.3 = `4/10 × 3/10=12/100`=0.12.
∴0.4× 0.3 =0.12

Method - 2:(Multiply and put decimals)
0.3 × 0.4
Step 1 : Multiply whole numbers ignoring decimals.
4 × 3 = 12

Step 2 : Mark the decimal point in the product from right most to left according to the total number of decimal places of the given numbers. Here it is two.
∴ 0.4 × 0.3 = 0.12

The number of decimal digits in the product of any two decimal numbers is equal to the sum of decimal digits that are multiplied.

Find the product of the following. i) 69.2 × 2.5 ii) 20.61 × 3.09 iii) 658.321 × 43.2 iv) 206.005 × 0.07

Solution :
i) 692 × 25 = 17300
  69.2 × 2.5 = 173.00

ii) 2061 × 309=636849
  20.61 × 3.09=63.6849

iii) 658321 × 432=284394672
   658.321 × 43.2=28439.4672

iv) 206005 ×7=1442035
   206.005 × 0.07=14.42035

---

EXAMPLES

---

If one side of a square is 3.8 cm, then find its perimeter?

Solution :
Number of sides to a square = 4
Each side of a square is equal.
Side of a square = 3.8 cm
∴ Perimeter of a square = 4 × side
= 4 × 3.8 = 15.2 cm

Find the product:

1) 32.5 × 8
325 × 8 = 2600
32.5 × 8 = 260.0

2) 94.62 × 7
9462 × 7=66234
94.62 × 7=662.34

3) 109.761 × 31
109761 × 31=3402591
109.761 × 31=3402.591

4) 61 × 2.39
61 × 239=14579
61 × 2.39=145.79

To multiply decimal numbers by 10, 100, 1000... just shift the decimal point in the product as many places to the right, as number of zeroes after 1.

Find i) 239.27 × 10 ii) 5.305 × 100 iii) 23.1 × 1000

Solution :
i) 239.27 × 10
number of zeroes in 10 is one. So, decimal point has to shift to one place right in the product.
∴ 239.27 × 10 = 2392.7

ii)5.305 × 100
number of zeroes in 100 is 2. So, the decimal point has to shift to 2 places right in the product.
∴5.305 × 100 = 530.5

iii) 23.1 × 1000
a number of zeroes in 1000 is 3. So, the decimal point has to shift to 3 places right in the product.
∴ 23.1 × 1000 = 23100.0 = 23100

Find i) 27.35 × 10,   ii) 27.35 × 100 and   iii) 27.35 × 1000

i) 27.35 × 10 = 273.5
ii) 27.35 × 100 = 2735
iii) 27.35 × 1000 = 27350

Find the values of the following . i) 26.59 × 10 ii) 206.5 ×100 iii) 206.5 × 1000 iv) 10.001 × 1000

i) 26.59 × 10 = 265.9
ii) 206.5 ×100= 20650
iii) 206.5 × 1000 =206500
iv) 10.001 × 1000=10001

Example : Bindu went to vegetable market with her mother to buy onions. If the cost of Onions is ₹18.50 per kg, then find the cost of 3.5 kg of Onions.

Solution :
Cost of 1 kg Onions = ₹18.50
Cost of 3.5 kg of Onions = 3.5 × ₹18.50 = ₹64.750
∴ Cost of 3.5 kg of Onions = ₹64.75

Example: One day Karthik went to petrol bunk to fill petrol in his car. If the cost of petrol is 783.21 per liter, then how much he has to pay to fill the full tank with 36.2 liters?

Solution : Cost of 1 litre petrol = ₹83.21
Cost of 36.2 litre petrol = 36.2 × ₹83.21
= ₹3012.202
∴ Cost of 36.2 litres of petrol = ₹3012.20

I am a decimal number, who is half of one-fourth of 100. Who am I?

fourth of a hundred is 25.
Half of 25 is 12.5
So, the decimal number is 12.5

---

EXERCISE- 2.2

---

1. Find the product of the following. i) 23.4 × 6 ii) 681.25 × 9 iii) 53.29 × 14 iv) 8 × 2.52 v) 25 × 2.013

Solution : i) 23.4 × 6 = 140.4
ii) 681.25 × 9 = 6131.25
iii) 53.29 × 14 = 746.06
iv) 8 × 2.52 = 20.16
v) 25 × 2.013 = 50.325

2. Fill the blanks in the table

3. Find the product.

i) 5.1 × 8.1

51 × 81=4131
5.1 × 8.1=41.31

ii) 63.205 × 0.27

63205 × 27=1706535
63.205 × 0.27=17.06535

iii) 1.321 × 0.9

1321 × 9=11889
1.321 × 0.9=1.1889

iv) 6.51 × 0.99

651 × 99=64449
6.51 × 0.99=6.4449

v) 837.6 × 0.006

8376 × 6=50256
837.6 × 0.006=5.0256

4. Rithesh reads a book for 2.5 hours everyday. If he reads the entire book in a Week, then how many hours all together are required for him read to the book?

Solution:
No. of hours Ritesh reads a book everyday =2.5 hours
No. of hours Ritesh reads the book in a week=2.5×7 = 17.5
Rithesh reads the book in 17.5 hours.

5. Find the area of the rectangle whose length and breadth are 5.3cm, 2.7cm respectively.

Solution:
Length =5.3cm
Breadth =2.7cm
Area of the rectangle =length × breadth
= 5.3 × 2.7 = 14.31 sq.cm

6. If the cost of each cement bag is ₹326.50, then find the cost of 24 bags of cement.

Solution:
Cost of a cement bag = ₹326.50
Cost of 24 cement bags = ₹326.50×24
=₹7836.00
∴ The cost of 24 bags of cement is ₹7836

7. Dharmika purchased chudidhar material of 1.40m at the rate of ₹152.5per meter. Find the amount to be paid.

Solution:
one meter material cost = ₹152.5
1.4 meter material cost = ₹152.5 × 1.4
=₹213.50
∴ The amount to be paid for 1.40 meter chudidhar material is ₹213.50

8. If a picture chart costs ₹4.25. Amrutha wants to buy 16 charts to make an album. How much money does she have to pay?

Solution:
Cost of a Picture chart = ₹4.25
Cost of 16 Picture charts = ₹4.25× 16
=68.00
∴ Amrutha has to pay = ₹68

<Exercise 1 Review Exercise >