Integers exercise 4 apscert class 7
BODMAS RULE
To simplify arithmetic expressions, a particular sequence of operations has to be followed. The hierarchy of arithmetic operations to be followed is given by a rule called BODMAS rule.
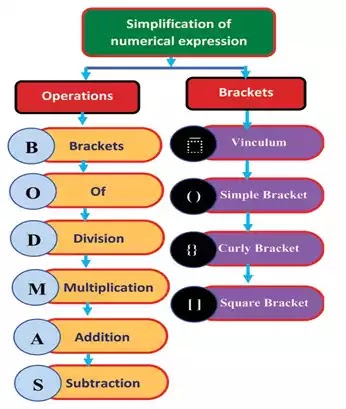
There are four types of brackets:
1.Vinculum:
This is represented by a bar on the top of the numbers.
Example:2 + 3 − 4 + 3. Here, the figures under the vinculum have to be calculated as 4 + 3 first and the ‘minus’ sign before 4 is applicable to 7. Thus, the given expression is equal to 2 + 3 − 7 which is equal to −2.
2.Simple Bracket:
This is represented by ( )
3. Curly Bracket:
This is represented by { }
4. Square Bracket:
This is represented by [ ]
EXAMPLES
Example 11 : Simplify 3 × 2 + 8 ÷ 4
Solution :3 × 2 + 8 ÷ 4 (Division)
= 3 × 2 + 2 (Multiplication)
= 6 + 2 (Addition)
= 8
Simplify the following.
(i) 5 × 6 – 6
Solution :5 × 6 – 6 (Multiplication)
=30– 6 (Subtraction)
= 24
(ii) 24 ÷ 3 × 3 – 30
Solution :24 ÷ 3 × 3 – 30 (Division)
=8× 3 – 30 (Multiplication)
=24– 30 (Subtraction)
=– 6
(iii) 5 × 5 – 5 ÷ 5 + 5
Solution :5 × 5 – 5 ÷ 5 + 5 (Division)
=5 × 5 – 1+ 5 (Multiplication)
=25– 1+ 5 (Addition)
=25–6 (Subtraction)
=19
Example 12 :Simplify 7 × 6 – 8 – 4
Solution :7 × 6 – 8 – 4 (Vinculum)
= 7 × 6 – 4 (Multiplication)
= 42 – 4 (Subtraction)
= 38
Example 13 :Simplify 18 + 64 ÷ 4 {26 – (14 – 7 – 3)}
Solution :18 + 64 ÷ 4 {26 – (14 – 7 – 3)} (Vinculum)
= 18 + 64 ÷ 4{26 – (14 – 4)} (Simple bracket)
= 18 + 64 ÷ 4{26 – 10} (Curly bracket)
= 18 + 64 ÷ 4 {16} (Of )
= 18 + 64 ÷ 64 (Division)
= 18 + 1 (Addition)
= 19
EXERCISE-4
=6 × 9 – 2 (Multiplication)
=54 – 2 (Subtraction)
=52
ii) 12 ÷ 4 – 8 + 5 (Division)
=3 – 8 + 5 (Addition)
=8 – 8 (Subtraction)
=0
iii) 80 – 56 ÷ 8 × 9 (Division)
=80 – 7 × 9 (Multiplication)
=80 – 63 (Subtraction)
=17
iv) 15 ÷ 5 + 17 – 30 (Division)
= 3 + 17 – 30 (Addition)
=20 – 30 (Subtraction)
=–10
v) 8 + 8 – 8 × 8 ÷ 8 (Division)
=8 + 8 – 8 ×1 (Multiplication)
=8 + 8 – 8 (Addition)
=16 – 8 (Subtraction)
=8
=8 × 3 – 6 (Multiplication)
=24 – 6 (Subtraction)
= 18
ii) {12 – 14 – 8 + 7} – 15 (Vinculum)
={12 – 6 + 7} – 15 (addition in Curly bracket)
={19 – 6 } – 15 ( Curly bracket)
= 13 – 15 (Subtraction)
= –2
iii) 16 – (4 + 18 ÷ 6 – 7 – 5) × 5
iv) {6 of 145 ÷ (3 + 2)} ÷2 – 4 of 20 (Simple bracket)
={6 of 145 ÷ 5} ÷2 – 4 of 20 (of in Curly bracket)
={870 ÷ 5} ÷2 – 4 of 20 ( Curly bracket)
=174 ÷2 – 4 of 20 (Division)
=87 – 80 (Subtraction)
= 7
v) 25 + [14 – 18 + {12 of 5 – (– 4 + 14)}] (Simple bracket)
=25 + [14 – 18 + {12 of 5 – 10}] (of in Curly bracket)
=25 + [14 – 18 + {60 – 10}] ( Curly bracket)
=25 + [14 – 18 + 50] (addition in Square bracket)
=25 + [64 – 18 ] ( Square bracket)
=25 + 46 (addition )
= 71
because 48 ÷ 6 – 4 = 8 – 4 = 4
ii) –18 + 12 ÷ 3 = –14 --True
because –18 + 12 ÷ 3 = –18 + 4 = –14
iii) –11 + 3 × 7 = –56--False
because –11 + 3 × 7 = –11 + 21 = 10
iv) 2020 ÷ 20 – 100 = 1--True
because 2020 ÷ 20 – 100 = 101 – 100 = 1
ii) –6 + 12 ÷ 6 = –4
iii) –15 ÷ 3 × 6 = –30

Post a Comment